APPARENT
LACK OF SYMMETRY IN STELLAR
ABERRATION AND EUCLIDEAN SPACE TIME
ABSTRACT :-
The
effect of stellar aberration seems to be one of the simplest phenomena
in astronomical observations. But there is a large literature about
it betraying a problem of asymmetry between observer motion and source
motion. This paper addresses the problem from the point of view of Euclidean
space-time, arising from the proposition that stellar aberration (or
Bradley aberration) gives rise to a Lorentz expansion.
( 1)
INTRODUCTION:-
It is known
that the earth completes a full circumference around the Sun every year.
Consequently, since the Earth-Sun radius (Re) is well known,
it is easy to determine the earth tangential velocity (Vt)
required to complete the circumference in twelve months (T seconds).
We have:
2 p
(Re) =(Vt)T [equation 4]
Equation
(4) predicts that the average translational velocity V of the earth
around the Sun is 29.79 Km/s. Of course, the earth velocity vector changes
continuously in direction and completes a full cycle during a one year
period while the earth circles the Sun.
On
Figure A [26], an observer on Earth detects the photons emitted by a
stationary star S, located in a direction perpendicular to the Earth
velocity Vt. The star is located at such a large distance
from the earth that the parallax caused by the orbit diameter around
the Sun is completely negligible. Only the transverse velocity matters
here. The stationary
star S is emitting photons in all directions. The Earth and the telescope
are moving upward at a velocity V . The telescope must make an angle q
with respect to the real direction of the arriving photons in order
to collect them at its focus.
In astronomy textbooks, the relative velocity between photons (at velocity
c) and the Earth (Vt), explains why a telescope on Earth
(see Fig. A) must be pointing at the angle q , with respect to the Earth-star direction,
to be able to point at the star. Figure A shows that while the photons
move in straight line toward the Earth, they will always remain in the
axis of an inclined telescope, since it is moving sideways with the
Earth. The angle q is
equal to:
Tan q
=(Vt)/c [EQUATIO
N 5]
Equation
(5) gives q
equals 20.5 arc-s. This is in perfect agreement with the value of aberration
observed so many times since Bradley[11] in 1727. During the year, the
observed direction of the stars makes one oscillation with an amplitude
of 20.5 arc-s., as expected from the Earth motion around the Earth.
The value of 20.5 arc-s. is called the constant of stellar aberration.
The equation (5) ,in fact, gives classical formula for aberration in
absolute time in which the waves (strictly the normals of the wave fronts)
are not subjected to aberration to the great disappointment of Fresnel
[1]. The relativity theory has solved this problem in terms of the
relativity of simultaneity. Equal aberration for light photons and
light waves requires this revision of simultaneity concept. Aberration
is understood as aberration of the wave front normals. Such an aberration
is the corollary of the relative simultaneity. According to Born [27],
the relativistic stellar aberration formula calculation with a wave-front
normal or phase through Lorentz transformation turned out to be identical
to that with a particle through Einstein’s composition rule for velocities.
Consequently, formulas are derived either by the first method in text
books [28-33], or by the second method in the text books [34-36]. Today,
the aberration is formally derived in text-books [6-8] from the relativistic
transformation of the phase. But in these text-books [6-8] and [28-33],
in the derivation of aberration from the relativistic transformation
of the phase, the inverse Lorentz transformation equations are used
as if one is going from moving frame to the rest frame. The preceding
statement becomes quite clear later on in Section 3 (Conclusion–2) where
on substituting inverse Lorentz transformation in place of Lorentz transformation
[equation (11)] in right hand side of equation (10) and on comparing
the coefficients of x, y, z and t in the resulting equation, the relativistic
stellar aberration formula is derived. Aberration can also be derived
from relativistic composition law of velocities which when applied in
moving frame of source, using inverse Lorentz Transformations, predicts
an aberration effect produced by the motion of the source in rest frame
as discussed below.
Consider
an inertial rest frame K with respect to which another inertial frame
K’ is moving with velocity v along x-axis in positive (+X) direction.
Further, consider a light photon emitted by a light source at rest in
frame K’ such that the direction of emission lies in x-y plane and makes
an angle q
and q’
with +Y- axis in frame K and K’ respectively. Using inverse Lorentz
transformations, the velocity components c cos q and c sin q of light photon along Y and X-axis
respectively in rest frame K are expressed in terms of velocity components
(c cos q’)
and (c sin q’)
in K’ as
c
sin q
= (c sin q’
+ v)/(1+v sin q’/c) ------(1)
c
cos q
= (c cos q’)/g(1+v
sin q’/c) where g
= 1/(1-v2/c2)0.5 ------(2)
Taking
ratio of (1) and (2), we get
Tan q
= g
(c sin q’
+ v)/(c cos q’) ------(3)
The
equation (3), derived using inverse Lorentz Transformation, predicts
active aberration effect produced by the motion of source in rest frame
K. This prediction is based on , relative motion between source and
observer, which is claimed to be the cause of aberration even by Einstein
[12] and Pauli [13]. But in the beginning of twentieth century, the
observational evidence for the lack of longitudinal additions to the
velocity of light by the radial motion of the source (Guthnick [14],
desitter [15], Zurhellen[16]), later improved for extragalactic objects
(Stromberg [17], Heckmann [18], Schmidt [19], Brecher [20], Barnet,
Davis and Sanders [21]), convinced about the observational absence of
active aberration. This absence was first tested by H. Seeliger [9]
and Nyren [10] and also, recently, some authors [22-25] have shown this
absence. This lack of observational confirmation of active aberration
was interpreted as an error in the theory of relativity and as a hint
that the latter had to be revised accordingly [2-5]. History forgot
their [2-5] argument because they failed to provide correct explanation
to the observed absence of active aberration. This revision of relativity
theory is in the form of Euclidean Space –time in place of the Einstein’s
four dimensional space time. Euclidean Space –time is such that both
relativistic transformation of the phase and relativistic composition
law of velocities make use of Lorentz transformations in deriving the
relativistic aberration and doppler formulas. Further, the statement
[1], that the aberration is a correction to be applied between observers
in relative motion, is self-evident in the Euclidean Space-time
Moreover,
the absence of active aberration leads to apparent lack of symmetry
in aberration i.e. aberration is observed when observer is moving and
not when source is moving. In order to find correct and rational explanation
for the observed absence of active aberration produced by the motion
of source, the mechanism of stellar aberration is reviewed in the next
section.
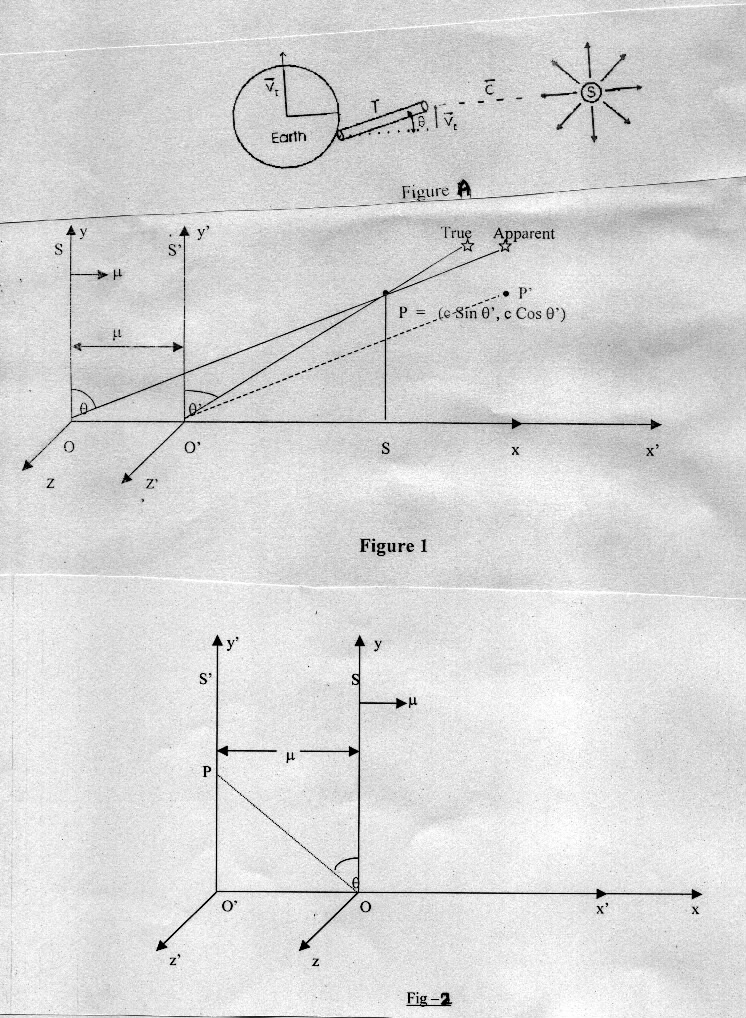
(2) MECHANISM
OF ABERRATION :
The
aberration of star light is as follows. Let us assume that the rest
frame S' of Fig. 1 is fixed by astronomical coordinates to the solar
system, with respect to which the frame S attached to the Earth is moving
towards right with orbital velocity m at time t' = -1 as shown in Fig.l.
Consider a starlight photon in S' at point P in the x' -
y' plane with x' and y' coordinates as c sin q'
and c cos q',
respectively. This photon would be observed simultaneously in
S and S' when O and O' coincide at t = t' = 0. Due to stellar aberration
[37] the observer O sees the incoming direction of the starlight photon
along line O'P' at t = t' = 0 such that PP' = m and point P' coincides the point P
at t' = -1. This coincidence of P and P' is possible only in classical
time concept, t = t', and not in Einstein’s new time concept, t = b
(t' + m
x' / c2) where b = 1/ (1 - m2/c2)0.5.
The problem lies in the fact that the stellar aberration as outlined
above can be explained only in classical time concept with which the
principle of constancy of light speed in S and S' is incompatible. It
is this incompatibility that lead Einstein to establish new time concept
[38]. Our endeavour is to find a time concept that explains stellar
aberration as well as principle of constancy of light speed in S and
S’.
In
frame S this photon approaches the point O along the straight line OP
which occupies the position O'P' in S' at t' = 0. But there is nothing
worth moving length*(In [39] Einstein defined the concept of moving length as “By means of stationary clocks set up in the stationary system and synchronizing in accordance with Einstein’s definition of simultaneity, the observer ascertains at what points of stationary system the two ends of the rod to be measured are located at a definite time. The distance between these two points, measured by the measuring rod already employed which in this case is at rest, is also a length which may be designated the length of the rod. The length to be discovered by the above operation, we will call the length of the (moving) rod in stationary system.) in Fig. 1 to substantiate the preceding
statement. In objective reality there are only rest lengths OP and O'P'
of S'. This means that the coinciding of O and O' at t = t' = 0 is accompanied
by dislocation of initial point P of starlight photon to the point P'
in S. In other words, the length OP at t'
= -1 is a moving length which moves to position O'P' at t'
= 0 in Fig. 1. But the principle of constancy of light speed in S and
S' demands that the moving length OP must be Lorentz contracted along
the direction of motion of S so that the rest length OP in S' reveals
itself as a dilated value rather than a contracted value in S. Moreover,
the dislocation of initial point P of starlight photon to point P' in
S implies that the relativity of simultaneity acquires meaning only
when the spatial and temporal axes coincide each other in S and S'.
In
Fig.1 the angle q
of tilt of the telescope to see the photon in the earth frame S can
be obtained by considering the rest length OS of the frame S' as Lorentz
contracted moving length of the earth frame S, and we get tan q
= OS / PS = b
(m
+ c sin q')
/ c cos q'
where b
= 1/ (1 - m2/c2)0.5.
This is the relativistic formula for the aberration of starlight which
was already deduced by Einstein in his first paper [40].
The formula for the angle of aberration, instead of being tan q
= m/c,
then becomes sinq
= m/c
when q’
= 0. The relativistic formula agrees with the classical formula for
quantities of first order in case of relative transverse velocity between
star and earth. Further, Let assuming that Fig. 2 represents. Fig.1
at time instant t’ = +1 such that q’ = 0. Additionally, there is present
at origin O of earth frame S a small horizontal plane mirror in x-z
plane that reflects the incoming star light photon at
t’ = t = 0. In accordance with laws of reflection the starlight photon
is reflected at angle sin q = m / c along OP in earth frame S and
at normal along O’P = c in frame S’ because of normal incidence in S’.
After reflection the earth becomes moving source that has emitted reflected
starlight photon at t = t’= 0. It is quite obvious that the direction
OP of outgoing reflected starlight photon in earth frame S is apparent
direction (as incoming starlight photon direction was apparent in S)
and the direction O’P of outgoing reflected starlight photon in frame
S’ is true direction. This implies that the earth frame S as moving
source with transverse velocity emits the reflected star-light photon
without any aberration. Consequently, the apparent lack of symmetry
(described in section 1 of this paper) in stellar aberration, when the
star is moving at transverse velocity, can be explained on the basis
of above discussion. The fact, that Einstein’s theory fails to explain
this lack of symmetry in aberration, implies that something is wrong
with Einstein’s theory. Let us see what new conclusions can be drawn
about relativity from the above discussion of stellar aberration that
explains apparent lack of symmetry in aberration.
(3)
CONCLUSION (1) :
The
angle q
of tilt of the telescope to see the photon in the earth frame S can
be obtained by considering the rest length OS of the frame S' as Lorentz
contracted moving length of the earth frame S, and we get tan q
= OS / PS = b
(m
+ c sinq
') / c cos q'
where b
= 1/ (1 - m2/c2)0.5.
This clearly establishes that the rest length OS in S' does reveal itself
as a dilated value in moving frame S in Fig. 1 rather than a contracted
value. Further, in Fig. 1 the point P is the origin of temporal axis
O'P in S' and of temporal axis OP in S for the starlight photon at P.
Due to stellar aberration the physical existence of these temporal axes
in S and S' can be experimentally proved in the form of apparent and
true star positions observed simultaneously in S and S' when O and O'
coincide at t = t' = 0 and observe the starlight photon previously at
point P. This implies that (a) the distinction between space and time
disappears completely. (b) there is no difference between time direction
[41] and space direction, (c) time should be measured in imaginary numbers
rather than real ones. On this basis the conclusion that space time
is Euclidean appears to be convincing and reasonable enough, since with
imaginary time it has a Euclidean metric.
Moreover,
the principle of relativity demands that the rest length in S must also
reveal itself as a dilated value in S'. This is possible only when frame
S also becomes Lorentz contracted along with frame S' when one moves
from frame S' to moving frame S in Fig. 1. This implies that the length
OO' = bm of
frame S in Fig. 1 becomes Lorentz contracted as OO' = m in going from frame S' to S in Fig.
1. This reveals another aspect of Euclidean space time that when rest
clock at O' registers
t'=-1 in Fig. 1, the observer at O adjusts itself spatially as well
as temporally on moving from S' to S so that the rest clock at O in
S registers t = -1.
CONCLUSION
(2)
In
Euclidean space-time the relativistic transformation of the phase and
relativistic composition law of velocities make use of Lorentz transformation
in deriving the relativistic aberration and doppler formulas as discussed
below.
In
Fig. 1 the length OP of moving frame S in Euclidean-space time is calculated
as
OP
= [OS2 + PS2] 0.5
Substituting
OS = b
(m
+ c sin q’)
and PS = c cos q’
in above equation, we get
OP
= b
(c + m
sin q’)
This
means that cosq
in S is represented in Euclidean space-time as
cos q
= (PS / OP) = (c cos q’)/ b (c + m sin q’) ------(6)
Keeping
in view the relativistic law of conservation of linear momentum, the
linear momentum components along Y – axis of the starlight photon in
frames S and S’ of Fig. 1 must be equal i.e.
(hw/2pc)
cos q
= (hw’/2pc)
cos q’ ------(7)
Where
h is planck’s constant and w, w’ are angular frequencies of starlight
photon in S and S’ respectively. Rearranging terms in equation (7) and
substituting equation (6) in (7), we get
w
= bw’
(1+m
cos q’/c)
------(8)
The
relation between wave-vectors k and k’ of starlight photon in frames
S and S’ of Fig.1 can be found easily by substituting w = ck and w’=ck’
in equation (8) and we get
k
= b
k’ (1+m
cos q’/c) ------(9)
Consider
a plane wave of frequency w’ and wave-vector k’ associated with the
starlight photon in frame S’ of Fig.1. In moving frame S of Fig.1 due
to linearity of Lorentz transformation this wave indeed remains a plane
wave but will have, in general, a different frequency w and wave vector
k but the phase f
of the wave is an invariant quantity.
wt
– k.r = f
= w’ t’ – k’.r’ -------(10)
Where
r and r’ are the radial motion vectors of starlight photon of Fig. 1
in frames S and S’ respectively.
If
we substitute equations (8) and (9) in left hand side (wt – k.r) of
equation (10) along with Lorentz transformation equations
x
= b
(x’ + mt’),
y = y’, z = z’ and t = b (t’+mx’/c2) -------(11)
we
get right hand side (w’t’ – k’.r’) of equation (10). This verification
of equation (10) leads to the result that the statement, for w and
k in equation (8) and (9), that are derived on the basis of Euclidean
space-time concept, represent angular frequency and wave-vector of starlight
photon in moving frame S and are in accordance with Lorentz transformation
equation. In fact, the equation (8) and (9) represent the relativistic
doppler effect statements derived on the basis of Euclidean space-time
concept. Moreover, the relativistic stellar aberration formula, derived
in Section 3(1) of this paper using Euclidean space-time concept, also
satisfies the Lorentz transformation equations (11).
Thus,
the above discussion leads to the result that Euclidean space-time is
such that both relativistic transformation of the phase and relativistic
composition law of velocities make use of Lorentz transformation in
deriving the relativistic aberration and doppler effect formulas.
(3)
CONCLUSION (3)
It
is stated in [1] that aberration is a correction to be applied between
observers in relative motion. This statement is self-evident in Euclidean
space-time concept as discussed below.
In
Fig. 1, if the velocity m of frame S is allowed to take an arbitrary
value between (-c) and (+c), the distance ( OO’ = m) is to be corrected for each observer
at O in relative motion in order to find the apparent stellar position
at angle q
in Euclidean space-time. This obviously leads to the result [1] that
aberration is a correction to be applied between observers in relative
motion.
REFERENCES
:
[1] D.-E.
Liebscher, P.Brosche, Bonn, Aberration and relativity, Astron.Nachr.319
(1998).
[5] Mohorovicic,
St. (1928) : Optik bewegter Korper, in : E.Gehrke, Handbuch der physikalischen
Optik 2, 917 ff., Leipzig, J.A. Barth.
[6] W.
Pauli, Theory of Relativity, p.19 (Pergamon Press, Oxford, 1958)
[7] Robert
Resnik, Introduction to Special Relativity, p.82 (Wiley Eastern Private
Limited, New Delhi, First Edition 1962, Reprinted 1972).
[8] J.D.
Jackson, Classical Electrodynamics, p.521 (Wiley Eastern Private Limited,
New Delhi, Second Edition 1975, Reprinted 1989).
[12] Einstein,
A. 1916, Uber spezielle und allgemeine Relativitatstheorie, Braunschweig,
Vieweg.
[21] Barnet,
C., Davis, R., Sanders, W.L. 1985, Astrophys. J. 295, 24-27.
[24] T.E.
Phipps “Relativity and Aberration,” Am. J. Phys., 57, pp., 549-550 (1989)
also Phipps T.E., Jr., “Stellar Aberration from the standpoint of the
Radiation Convection Hypothesis.” Phys. Essays 4, 368, (1991).
[26] Paul
Marmet, Stellar Aberration and Einstein’s Relativity, Physics Essays,
Vol. 9, No : 1p.96-99, 1976.
[29] Joos,
G. 1956, Lehrbuch der theoretischen Physik, Leipzig, Geest & Porting,
9.Aufl.
[30] Herlt,
E., Salie, N. 1978, Spezielle Relativitatstheorie, Berlin, Akademie-Verlag.
[31] Sommerfeld,
A. 1959, Vorlesungen, IV. Optik, 2. Aufl., Leipzing, Geest & Portig.
[34] Landau,
L.D., Lifshic, E.M. 1962, Klassische Feldtheorie, Berlin, Akademie-Verlag
1964.
[35] Goenner,
H. 1996, Einfuhrung in die spezielle and allgemeine Relativitatstheorie,
Heidelberg, Spektrum AV.
[36] Rindler,
W. 1986, Essential Relativity, Heidelberg, Springer.
[37] Albert
B. Stewart, The Discovery of Stellar Aberration, Scientific American,
p.100. (March, 1964).
[38] Harald
Nordenson, Relativity, Time and Reality, p.84 (George Allen and Unwin
Ltd., Ruskin House, Museum Street, London 1969).
[39] Albert
Einstein, On the Electrodynamics of Moving Bodies, Ann. Physik, 17,
891 (1905).
[40] W.
Pauli, Theory of Relativity, p.17 (Pergamon Press, Oxford, 1958).
[41] Stephen
Hawking, A Brief History of Time, p.142, (Bantam Press Edition reprinted,
1996).
Rajan
Dogra, Instructor, Wireless Operator Trade Industrial Training Institute,
Chandigarh.
Mail:
House No. 3291, Sector 27-D,
Chandigarh - 160 019, India
Phone : 0091-172-650148
E-mail: rajandogra@mailcity.com