|
|
|
COPYRIGHT
RAJAN DOGRA
ABSTRACT
The stellar aberration finds explanation in classical time concept with which the principle of constancy of light speed in all inertial frames is incompatible. It is the Euclidean nature of space time that explains stellar aberration as well as principle of constancy of light speed in vacuum.
(PACS 03.30. + P, 04.20. Gz)
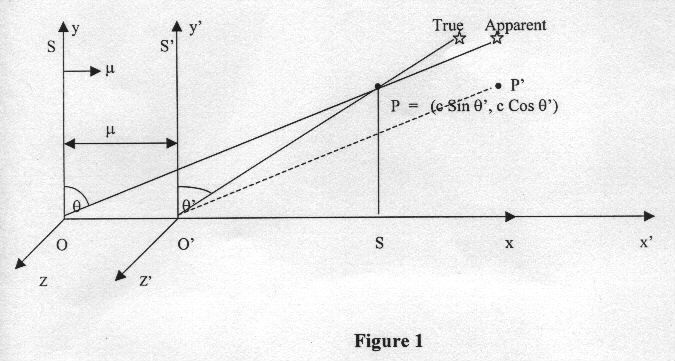
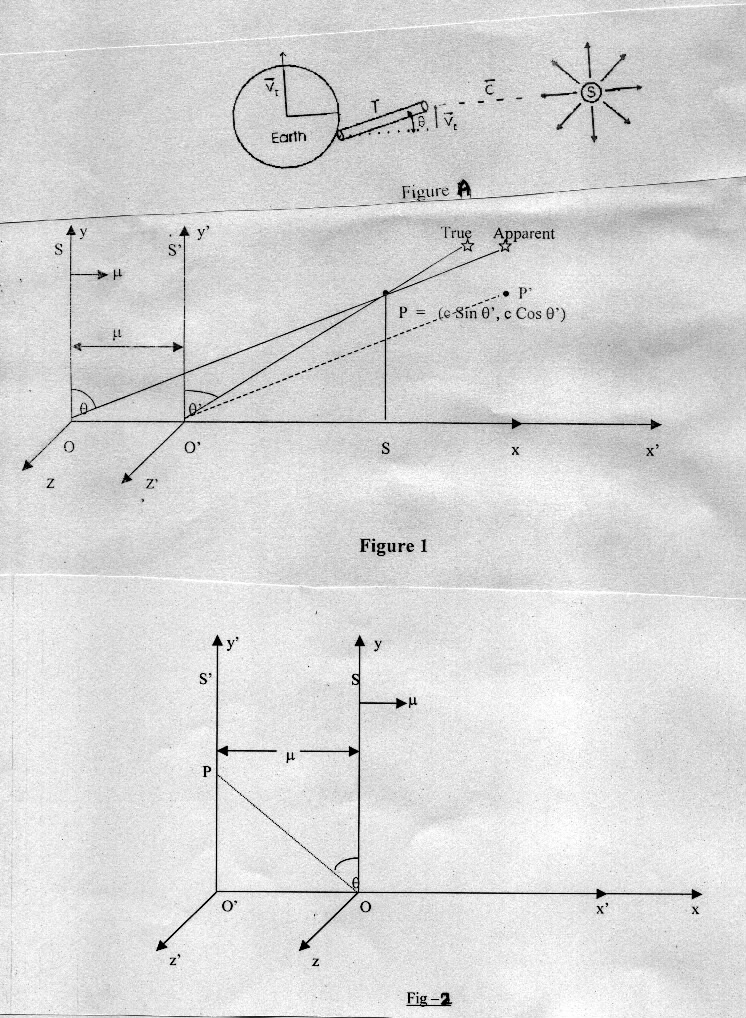
The aberration of star light, first reported by Bradley in 1727, is as follows. Let us assume that the rest frame S' of Fig. 1 is attached with astronomical coordinates fixed with the solar system, with respect to which the frame S attached with the earth is moving towards right with orbital velocity m at time instant t' = -1 as shown in Fig.l. Consider a starlight photon in S' at point P in the x' - y' plane with x' and y' coordinates as c sin q' and c cos q', respectively. This photon would be observed simultaneously in S and S' when O and O' coincide at t = t' = 0. Due to stellar aberration [1] the observer O sees the incoming direction of the starlight photon along line OP' at t = t' = 0 such that PP' = m and point P' coincides the point P at t' = -1. This coincidence of P and P' is possible only in classical time concept, t = t', and not in Einstein’s new time concept, t = b (t' + m x' / c2) where b = 1/ (1 - m2/c2)0.5. The problem lies in the fact that the stellar aberration as outlined above can be explained only in classical time concept with which the principle of constancy of light speed in S and S' is incompatible. It is this incompatibility that lead Einstein to establish new time concept [2]. Our endeavour is to find a time concept that explains stellar aberration as well as principle of constancy of light speed in S and S’.
In frame S this photon approaches the point O along the straight line OP which occupies the position O'P' in S' at t' = 0. But there is nothing worth moving length in Fig. 1 to substantiate the preceding statement. In objective reality there are only rest lengths OP and O'P' of S'. This means that the coinciding of O and O' at t = t' = 0 is accompanied by dislocation of initial point P of starlight photon to the point P' in S. In other words, the length OP at t' = -1 is a moving length which moves to position O'P' at t' = 0 in Fig. 1. But the principle of constancy of light speed in S and S' demands that the moving length OP must be Lorentz contracted along the direction of motion of S so that the rest length OP in S' reveals itself as a dilated value rather than a contracted value in S. Moreover, the dislocation of initial point P of starlight photon to point P' in S implies that the relativity of simultaneity has got meaning only when the spatial and temporal axes coincide each other in S and S'.
The angle q of tilt of the telescope to see the photon in the earth frame S can be obtained by considering the rest length OS of the frame S' as Lorentz contracted moving length of the earth frame S, and we get tan q = OS / PS = b (m + c sinq') / c cos q' where b = 1/ (1 - m2/c2)0.5. This is the relativistic formula for the aberration of starlight which was already deduced by Einstein in his first paper [3]. This clearly establishes that the rest length OS in S' does reveal itself as a dilated value in moving frame S in Fig. 1 rather than a contracted value. Further, in Fig. 1 the point P is the origin of temporal axis O'P in S' and of temporal axis OP in S for the starlight photon at P. Due to stellar aberration the physical existence of these temporal axes in S and S' can be experimentally proved in the form of apparent and true star positions observed simultaneously in S and S' when O and O' coincide at t = t' = 0 and observe the starlight photon previously at point P. This implies that (a) the distinction between space and time disappears completely. (b) there is no difference between time direction and space direction, (c) time should be measured in imaginary numbers rather than real ones. On the basis of these implications the conclusion that space time is Euclidean appears to be convincing and reasonable enough, since with imaginary time it has a Euclidean metric.
Moreover, the principle of relativity demands that the rest length in S must also reveal itself as a dilated value in S'. This is possible only when frame S must also get Lorentz contracted along with frame S' when one moves from frame S' to moving frame S in Fig. 1. This implies that the length OO' = bm of frame S in Fig. 1 gets Lorentz contracted as OO' = m when one goes from frame S' to S in Fig. 1. This reveals another aspect of Euclidean space time that when rest clock at O' registers t'= -1 in Fig. 1, the observer at O adjusts itself spatially as well as temporally when one moves from S' to S so that the rest clock at O in S registers t = -1.
References
[1] Albert B. Stewart, The Discovery of Stellar Aberration, Scientific American, p.100.(March, 1964)
[2] Harald Nordenson, Relativity, Time and Reality, p.84 (George Allen and Unwin Ltd., Ruskin House, Museum Street, London 1969).
[3] W. Pauli, Theory of Relativity, p.l7 (Pergamon Press, Oxford, 1958).
Rajan Dogra, Instructor, Wireless Operator Trade Industrial Training Institute, Chandigarh.
Mail:
House No. 3291, Sector 27-D,
Chandigarh - 160 019, India
Phone : 0091-172-650148
E-mail: rajandogra@mailcity.com
COPYRIGHT
RAJAN DOGRA
APPARENT
LACK OF SYMMETRY IN STELLAR
ABERRATION AND EUCLIDEAN SPACE TIME
ABSTRACT :-
( 1) INTRODUCTION:-
It is known that the earth completes a full circumference around the Sun every year. Consequently, since the Earth-Sun radius (Re) is well known, it is easy to determine the earth tangential velocity (Vt) required to complete the circumference in twelve months (T seconds). We have:
Equation (4) predicts that the average translational velocity V of the earth around the Sun is 29.79 Km/s. Of course, the earth velocity vector changes continuously in direction and completes a full cycle during a one year period while the earth circles the Sun.
On Figure A [26], an observer on Earth detects the photons emitted by a stationary star S, located in a direction perpendicular to the Earth velocity Vt. The star is located at such a large distance from the earth that the parallax caused by the orbit diameter around the Sun is completely negligible. Only the transverse velocity matters here. The stationary star S is emitting photons in all directions. The Earth and the telescope are moving upward at a velocity V . The telescope must make an angle q with respect to the real direction of the arriving photons in order to collect them at its focus.
(2) MECHANISM OF ABERRATION :
The formula for the angle of aberration, instead of being tan q
= m/c,
then becomes sinq
= m/c
when q’
= 0. The relativistic formula agrees with the classical formula for
quantities of first order in case of relative transverse velocity between
star and earth. Further, Let assuming that Fig. 2 represents. Fig.1
at time instant t’ = +1 such that q’ = 0. Additionally, there is present
at origin O of earth frame S a small horizontal plane mirror in x-z
plane that reflects the incoming star light photon at
t’ = t = 0. In accordance with laws of reflection the starlight photon
is reflected at angle sin q = m / c along OP in earth frame S and
at normal along O’P = c in frame S’ because of normal incidence in S’.
After reflection the earth becomes moving source that has emitted reflected
starlight photon at t = t’= 0. It is quite obvious that the direction
OP of outgoing reflected starlight photon in earth frame S is apparent
direction (as incoming starlight photon direction was apparent in S)
and the direction O’P of outgoing reflected starlight photon in frame
S’ is true direction. This implies that the earth frame S as moving
source with transverse velocity emits the reflected star-light photon
without any aberration. Consequently, the apparent lack of symmetry
(described in section 1 of this paper) in stellar aberration, when the
star is moving at transverse velocity, can be explained on the basis
of above discussion. The fact, that Einstein’s theory fails to explain
this lack of symmetry in aberration, implies that something is wrong
with Einstein’s theory. Let us see what new conclusions can be drawn
about relativity from the above discussion of stellar aberration that
explains apparent lack of symmetry in aberration.
(3) CONCLUSION (1) :
t'=-1 in Fig. 1, the observer at O adjusts itself spatially as well
as temporally on moving from S' to S so that the rest clock at O in
S registers t = -1.
(3) CONCLUSION (3)
[1] D.-E. Liebscher, P.Brosche, Bonn, Aberration and relativity, Astron.Nachr.319 (1998).
[2] Hayn, A.N. (1920) : Didaktisches zur Aberration II, Astron.Nachr.212, 81-88 (5070).
[3] Tomaschek, R. (1925) : Uber die Aberration, Z.Physik 32, 397-402.
[4] Osten, H.(1925) : Aberration und Relativitat, Astron.Nachr.224, 66-67 (Nr.5356).
[5] Mohorovicic, St. (1928) : Optik bewegter Korper, in : E.Gehrke, Handbuch der physikalischen Optik 2, 917 ff., Leipzig, J.A. Barth.
[6] W. Pauli, Theory of Relativity, p.19 (Pergamon Press, Oxford, 1958)
[7] Robert Resnik, Introduction to Special Relativity, p.82 (Wiley Eastern Private Limited, New Delhi, First Edition 1962, Reprinted 1972).
[8] J.D. Jackson, Classical Electrodynamics, p.521 (Wiley Eastern Private Limited, New Delhi, Second Edition 1975, Reprinted 1989).
[9] Seeliger, H. 1884, Astron.Nachr. 109, 275-280 (2610).
[10] Nyren, M. (1888) : Zur Aberration der Fixsterne, Bull. Acad.Imp.St. Petersburg 32, 402-412.
[11] J. Bradley “Account of a New Discovered Motion of the Fixed Stars” Phil. Trans. 35p.637 (1728).
[12] Einstein, A. 1916, Uber spezielle und allgemeine Relativitatstheorie, Braunschweig, Vieweg.
[13] Pauli, W. 1921, Enzyklopadie der mathematischen Wissenschaften V/2, S.563.
[14] Guthnick, P.1913, Astron.Nachr. 195, 265-272 (4670).
[15] deSitter, W. 1913, Phys.Z. 14,429.
[16] Zurhellen, W.1914, Astron.Nachr.198, 1-10 (4729).
[17] Stromberg, G.1931, Publ.Astr.Soc.Pacific 43, 266.
[18] Heckmann, O. 1960, Ann. d' Astrophysique 23, 168-173.
[19] Schmidt, Th. 1964, Z.Astrophys. 60, 106-111.
[20] Brecher, K. 1977, Phys.Rev.Lett. 39, 1051-1054.
[21] Barnet, C., Davis, R., Sanders, W.L. 1985, Astrophys. J. 295, 24-27.
[22] H.E. Ives “Extrapolation from the Michelson-Morley Experiment” J.Opt. Soc. Am. 40, pp. 185-190 (1950).
[23] E. Eisner, “Aberration of Light from Binary Stars – a Paradox?” Am. J. Phys. 35, pp.817-819 (1967).
[24] T.E. Phipps “Relativity and Aberration,” Am. J. Phys., 57, pp., 549-550 (1989) also Phipps T.E., Jr., “Stellar Aberration from the standpoint of the Radiation Convection Hypothesis.” Phys. Essays 4, 368, (1991).
[25] H.C. Hayden, Stellar Aberration, “Galilean Electrodynamics, 4.pp. 89-92 (1993).
[26] Paul Marmet, Stellar Aberration and Einstein’s Relativity, Physics Essays, Vol. 9, No : 1p.96-99, 1976.
[27] Born, M. 1920, Die Relativitatstheorie Einsteins, Vieweg Verlag Braunschweig.
[28] Bohm, D. 1965, The special theory of relativity, W.A. Benjamin.
[29] Joos, G. 1956, Lehrbuch der theoretischen Physik, Leipzig, Geest & Porting, 9.Aufl.
[30] Herlt, E., Salie, N. 1978, Spezielle Relativitatstheorie, Berlin, Akademie-Verlag.
[31] Sommerfeld, A. 1959, Vorlesungen, IV. Optik, 2. Aufl., Leipzing, Geest & Portig.
[32] Schneider, M. 1979, Himmelsmechanik, BI Mannheim.
[33a] Varicak 1910, Phys. Z.11, 93-96.
[33b] Varicak 1910, Phys. Z.11, 287-294.
[33c] Varicak 1910, Phys. Z.11, 586-587.
[34] Landau, L.D., Lifshic, E.M. 1962, Klassische Feldtheorie, Berlin, Akademie-Verlag 1964.
[35] Goenner, H. 1996, Einfuhrung in die spezielle and allgemeine Relativitatstheorie, Heidelberg, Spektrum AV.
[36] Rindler, W. 1986, Essential Relativity, Heidelberg, Springer.
[37] Albert B. Stewart, The Discovery of Stellar Aberration, Scientific American, p.100. (March, 1964).
[38] Harald Nordenson, Relativity, Time and Reality, p.84 (George Allen and Unwin Ltd., Ruskin House, Museum Street, London 1969).
[39] Albert Einstein, On the Electrodynamics of Moving Bodies, Ann. Physik, 17, 891 (1905).
[40] W. Pauli, Theory of Relativity, p.17 (Pergamon Press, Oxford, 1958).
[41] Stephen Hawking, A Brief History of Time, p.142, (Bantam Press Edition reprinted, 1996).
Rajan Dogra, Instructor, Wireless Operator Trade Industrial Training Institute, Chandigarh.
Mail:
House No. 3291, Sector 27-D,
Chandigarh - 160 019, India
Phone : 0091-172-650148
E-mail: rajandogra@mailcity.com
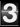

Author’s note:AS ONE GOES THROUGH MY PAPER THE FOLLOWING POINTS OF MISUNDERSTANDING ,CONFUSION AND PUZZLE ARE MOST LIKELY TO CROP UP IN ONE'S MIND.MY REJOINDER TO THESE POSSIBLE POINTS OF MISUNDERSTANDING
AND CONFUSION IS ALSO STATED BELOW.
(1.) The goal of this paper is to reconcile the experimental fact that the speed of light is
identical in any inertial frame with the Newtonian concept of absolute time. It is clear that what the author attempts do to is like the quadrature of the circle, that is, it is impossible.
MY REJOINDER :- >In my paper the statement "--The problem lies in the fact that the stellar aberration as outlined above can be explained only in classical time concept with which the principle of constancy of light speed in S and S' is incompatible --- " refutes the observation that the goal of my paper is to reconcile the experimental fact that the speed of light is identical in any inertial frame with the Newtonian concept of absolute time (read classical time concept). The observation that what the author attempts to do is like the quadrature of the circle, that is, it is impossible, and this impossibility is also stated in my paper when I state that the classical time concept and the principle of constancy of light
speed in S and S' are incompatible. (2.) The special theory of relativity is built on the observed constancy of the speed of light.With the additional assumptions of homogeneity and isotropy of space and homogeneity of time, the Lorentz transformations, viz. the relations between the coordinates of space-time events in two different inertial frames, can be derived by purely mathematical deduction. Length
contraction, time dilation {and the relativity of time} all are consequences of the Lorentz tranformations. One cannot have one and not the other. That is to say, one cannot have length contraction and also Newtonian time.It appears that the author is doing the same in
his paper. However, the author is basing many of his arguments on contracted or dilated lengths without any reference to the context from which this concept originates. Moreover, one has to be careful about applying, e.g., the term "length contraction". In the usage of special
relativity it means that the length of a meter stick at rest if measured
from a moving system { at a specified time in the moving system} will be contracted. In contrast, the author is using "length contraction" in a very haphazard way.One is puzzled by what exactly the author has in mind when he speaks of the``Euclidean nature of space-time''. He states that ``... time should be measured in imaginary numbers...." If so, then a Euclidean nature
of space-time implies that the sace-time interval squared is invariant, i.e., has the same
value in any inertial frame. However,the space-time interval squared whose invariance expresses the constancy of the speed of light in special relativity , has, as mentioned above, the Lorentz transformations as inescapable consequence and,therefore, forces one to abandon Newtonian absolute time. If the author wants to find an alternative to special relativity that is compatible with Newtonian time, then he has to set up an alternative to the Lorentz transformation from system S to system S', such that the speed of light is invariant and t= t'. This is like the quadrature of the circle. MY REJOINDER :-In my paper the statement "--But the principle of Constancy of light speed in S and S' demands That the moving length OP must be Lorentz Contracted ---"
clearly reveals that my arguments on contracted or dilated lengths originates from the concept of special theory of relativity of which the principle of constancy of light speed in any inertial frame is first postulate. The only point of difference between my arguments and special theory of relativity is the concept of moving length. In my arguments I am describing the path followed by starlight photon in earth frame S as moving length whereas the usage of special relativity describes the length of a moving materialistic object as moving length. My description of moving length is substantiated by the derivation of the relativistic stellar aberration formula on the basis of my description of moving length. Further, my description of moving length leads to coinciding of the spatial and temporal axes something unheard in usage of special relativity. This coincidence of spatial and temporal axes means that two points on X-axis having spatial separation equal to c ( i.e. the speed of light in vacuum) are not at same time instant but are having temporal separation of one second. This is what I meant by Euclidean nature of space-time. In this Euclidean nature of space-time the special theory of relativity
encompassing the principle of constancy of light speed in any inertial frame still holds good along with Lorentz transformations and consequences flowing from these transformations (viz length contraction, time dilation, etc.) In this context the statement of my paper, that
the rest length OS in S' reveals itself as a dilated value rather than a contracted value in S, is nothing but time dilation because the rest length divided by light speed in vacuum denotes temporal separation in Euclidean Nature of space-time.Further, the invariance of space-time interval squared has got no meaning in Euclidean Nature of space-time because the space and
time are on same footing in Euclidean space-time. The another consequence of Euclidean space -time is that time is indistinguishable from directions in space, i.e. if one can go east, one can turn around and head west; equally if one can forward in time, one ought to be able to turn around and go backward because spatial and temporal axes coincide each other in Euclidean space - time. This means that the spatial adjustment of observer O in last sentence of my paper
is equivalent to temporal adjustment when one moves from S' to S. (3)Please draw a Minkowskian plane (looks(!) like a
Euclidean plane) with horizontal axis x and vertical axis t.
Let Z=(0,0) S=(1,2) E=(0,4)Mark these points in the diagram and then connect
(with straight lines) ZE (along the t-axis),
ZS and SE so that you get a triangle.
Using the Minkowski metric (ds^2 = dx^2 - dt^2)(Euclidean: ds^2 = dx^2 + dt^2 ),
please calculate the "Minkowski Length" of the
lines ZE, ZS and SE and convince yourself that
ZE > ZS + SE (and post the solution !?).
Of course, the cat is out of the bag: you will have noticed that you're only
solving the twin "paradox".ZE is the worldline of the twin "at home", while
ZS + SE is the worldline of the intrepid traveller from Z (earth at 00:00
hours) to S (star) and back to E (earth at the end). The travel speed is
obvious, or is it ??
(If this is too boring, please prove that ZE is the LONGEST possible path
from Z to E; reminder: Z-to-E MUST be timelike throughout !)MY REJOINDER:-Euclidean plane is not like Minkowskian plane because Euclidean space-time is to be drawn with horizontal x-axis and horizontal t-axis coinciding each other.This means that two points on x-axis having spatial separation equal to light speed 'c' in vacuum are not at same time instant but are having temporal separation equal to one second. Consequently, When Z = (0,0) and S = (1,1) ,then Z and S are on x-axis but at different time instants in Euclidean space-time. When intrepid traveller starts from Z with travel speed equal to half of light speed , also assume that a light photon also starts from Z towards star S. When traveller reaches star S =(1,3) ,the light photon reaches at P = (2,2) on x-axis. In Euclidean space-time the path SP followed by photon on x-axis is moving length that is transversed by the star S to reach the intrepid traveller in the frame of traveller. Therefore, the point P =(2,2) indicates initial star position in traveller 's frame. Accordingly,the Euclidean length should be calculated by joining Z and P and not Z and S . Therefore, The Euclidean length ZP is equal to time like length (0,2) that elapsed at Z in forward journey of intrepid traveller. Same argument is applicable to backward journey.
Tell me what you think of the given
experimental proof of Euclidean nature of Space- time. Send me your mail to E-mail: rajandogra@mailcity.com
Mathematical Contradiction of Special
Relativity (By Eric J. Lange) and
Euclidean Space -Time
Einstein based his special theory of relativity on two
postulates:
1. The laws of physics are the same in all inertial
systems (reference frames that move uniformly and without rotation). There are
no preferred inertial systems. When a certain reference-frame moves with
constant speed with respect to another, processes of nature will obey the same
laws of physics in either reference-frame.
2. The speed of light in vacuum has the same constant
value c in all inertial systems.
Let a light signal travels along X-axis with speed
c in rest frame C such that x =
ct
The same light signal travels,
according to Einstein, also with respect to reference-frame C' with a speed
equal to c. With respect to C' the equation for the movement of the
light signal becomes: x'= ct '
The movement of frame C' with respect to frame C is
described by: a = v t
(For the three equations above and all still to
derive, applies that C' coincides with C at t = 0 and t' = 0. The covered
distances x and x' of the light signal are at that moment also equal to zero.)
Einstein had to make concessions in relation to
absolute time which was generally accepted back then. Because distances x and
x' (for t>0) were obviously not equal, t and t' had to be different too.
x = ct
x' = c t'
x' < x
c' = c
t' < t
The result of Einstein's principle of the constancy of
the speed of light, was therefore that the course of time in C and C' had to be
different. A clock would run slower in C' than in C.
The following derivation of the Lorentz-transformation
according to the special theory of relativity, is probably the most frequently
occurring version of the derivation of the transformation-equations that can be
found in the literature1, 2. It is this version that is taught on
universities around the world.
The light signal moves uniformly rectilinear with
respect to both reference-frames. This means there exists a linear relation
between coordinates x, y, z, t and x', y', z', t'. The most common form of this
relation is as follows:
|
X' = a11
x + a12 y + a13 z + a14 t (1) y' = a21
x + a22 y + a 23z + a 24t (2) z' = a31
x + a32 y + a33 z + a 34t (3) t' = a41 x + a 42 y + a
43 z + a 44
t (4) Because C' moves linearly along the
x-axis of C, it always applies that y=y' and z=z'. From this follows for the
coefficients: a21 = a 23 = a 24 = a31 = a32
= a34 = 0 a 22 = a33 = 1 Because of symmetry reasons t' can only
depend on x and t. From this follows: a42 = a 43 = 0 Then it is assumed that x'=0 in C' has to correspond
with x = vt in C. It follows for the coefficients that: a12 = a 13 = 0 a14 = -v a11 When the coefficients in equations (1), (2), (3) and
(4) are substituted by there values we get: x' = a11
(x - v t) (5) y' = y (6) z' = z (7) t' = a 41
x + a 44 t (8)
The falsity in this derivation can be located in the
assumption that x'=0 has to correspond with x = v t. At t=t'=0, when x=0, x' will be equal to zero too.
In a small time-interval greater than zero the speeds of C' and the light
signal can be defined. As determined before, x is defined as the distance a
light signal travels with speed c during a time interval t, and a
the distance C' travels with speed v. With x = v t it has
become unclear what movement we are talking about: 1. When it is meant to describe the propagation of
light, it is not proper to use the variable v in this equation, since
it equals the constant c (always). Substituting occurrences of v by c in this derivation shows clearly that this makes the
transformation equations meaningless and useless. 2. It is more likely that v is intended to describe
the movement of coordinate-system C', as was determined before. In the
schematic figures and derivations I have seen, the speed v was never
determined beforehand as being a divided by t, like I did in this
article. v is usually left undetermined (although definitely
designated to the speed of C') up to the point where the assumption is being
made that x'=0 has to correspond with x = v t. I wanted to make clear
from the start that the distance C' travels should not be described by x since
this variable already describes the distance light travels. Therefore it can
now be absolutely clear that x may not be used in this equation when it
describes the movement of C'. Using the same variable x for different
distances corrupts the derivation and makes it false. (When we would assume
that C' and the light signal always coincide, so that a = x and the equation
becomes justified, then v = c and the problem arises that their
coinciding is contradictory to the second postulate.) Thus the equation x = v
t is inconsistent with the assumptions on which the whole derivation is
based, which falsifies the results as derivatives of the two postulates of
the special theory of relativity. The mistake which was being made in the assumption that
led to equations (5), (6), (7) and (8) do indeed show up in those equations.
Specifically in equation (5) an error can be found, for in equation (5) a11
can't be solved (as is intended later on): x' = 0 x - vt = 0 x' = a11
(x - vt) a11 = 0/0 For the sake of completeness, the rest of the
derivation will be shown in short. When a light signal is transmitted in
arbitrary direction at t=t'=0, then the covered distance of the signal with
respect to C can be determined with Pythagoras and satisfies therefore: x2 + y2 + z 2 - c2
t 2 = 0 (9) With respect to C' applies: x2
+ y'2 + z' 2
- c 2 t'2
= 0 (10) Substitution of equations (5), (6),
(7) and (8) in equation (10) gives: X 2 (a 211 - c2
a 241) - 2 xt (a 211 v + a41 a44 c2) +
y2 + z2 - t2 (a244 c2 - a211 v2) =
0
(11) Equation of (9) and (11) leads to the next three
equations for determining a11, a41 and a44: a 211 - c2 a 241
= 1 a211 v +
a41 a44 c2 = 0 a244 c2 - a 211 v2 =
c2 a11
= a44 = 1 / (1-v2/c2) 0.5 (12) a 41 = -v/c2 (1-v2/c2) 0.5 (13) In deriving (12) and (13), the signs (- or +) are
chosen so that when v becomes equal
to zero (!), the equations (5), (6), (7) and (8) change into: x' = x y' = y z' = z t' = t Substitution of equations (12) and (13) in (5), (6),
(7) and (8) gives the Lorentz-transformation: x' = (x - vt) b
Where b
= 1 / (1-v2/c2) 0.5 (14) y' = y z' = z t' = (t
- vx/c2) b (15) (H.A.Lorentz derived equations (14) and (15) first
(based on an ether theory), years before Einstein first published his special
relativity theory.) Summarizing, I think the mathematical error in the
above derivation can be located where c
is falsely substituted by v (or where x is wrongly equated to vt).
The concluding transformation equations may appear alright but note that v entered those equations unjustified.
Replacing this variable with c in
(14) en (15) shows the falsity of this derivation convincingly. The derivations of the Lorentz-transformation by
Einstein himself (in his original article3 and much later in
another and also "simplified" form in his book about relativity4 )
contain the same error as in the above derivation. The falsity of these derivations does not prove of
course that in principle a good derivation can't be made at all. A proof of
this sort lies more on a philosophical en empirical plane I think. I
consider, for instance, the postulate of the constant speed of light to be in
contradiction with Galilean transformation and therefore false. The
relativity of speeds in general makes one absolute speed impossible, whilst
the postulate itself should make usage of Galilean transformation in the
derivation of the relativistic transformation equations out the question.
Yet, all of the derivations are based on Galilean transformation. Furthermore
and foremost, I think it should be obvious to those who know the
Kennedy-Thorndike experiment5 (an altered version of the famous
Michelson-Morley experiment) that the relativistic transformation equations
can never explain or describe the results thereof. __________________ Erik J. Lange __________________ 1. Introduction to Special Relativity, R. Resnick,
J. Wiley & sons Inc., 1968 2. Klassieke Mechanica en Relativiteitstheorie,
J.J.J. Kokkedee, Uitg. T.U. Delft, 1992 3. A. Einstein, "Zur elektrodynamik bewegter
Körper", Annalen der Physik. IV. Folge. 17, page 891, 1905. 4. Relativiteit, speciale en algemene theorie, A.
Einstein, Het Spectrum, 1978 5. R.J. Kennedy and E.M.Thorndike, "Experimental establishment
of the relativity of time", the Physical Review, vol. 42, second series, page
400, 1932. My
explanation
The Mathematical error in the above derivation of
Lorentz transformation equation is
located where c is falsely substituted by
v as viewed by Eric J. Lange. But in Euclidean space - time the path
followed by light signal in moving frame C' is the moving length and
therefore (x - vt) denotes the moving length that is transversed by the light
signal with speed c. The initial point
x' = 0 of this moving length has to
be denoted by x = vt because the moving length itself is defined by the path transversed by the light signal with
speed 'c'. Therefore, it is clear that there is no mathematical error in the
derivation of Lorentz transformation equations in Euclidean space time when c
is substituted by v (or x is equated
to vt) |